Sets

While the developer documentation on $sets and the +in core is comprehensive, it is organized alphabetically which can make it difficult to see what's going on with set relations. This article will describe set identities and relations through the Hoon standard library.

A $set is a tree with a particular internal order based on the hash of the value. This tends to balance the values and make lookup and access more efficient over large sets.

Set Creation & Membership

Define a Set

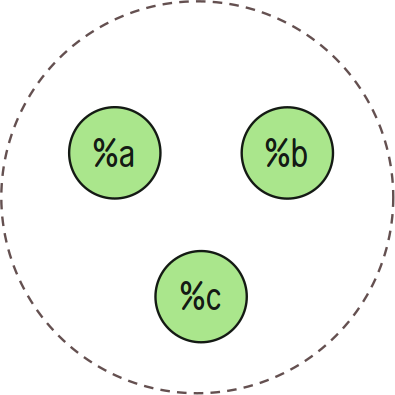
++silt produces a $set from a $list.

> `(set @tas)`(silt `(list @tas)`~[%a %b %c %a])
{%b %a %c}

Add Members

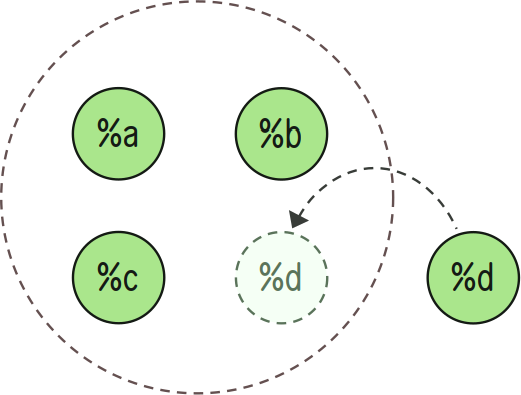
++put:in adds an element x to a set A.

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  `(set @tas)`(~(put in a) %d)
{%b %d %a %c}

++gas:in adds each element x, y, z of a list to a set A.

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  =/  b  `(list @tas)`~[%d %e %f]
  `(set @tas)`(~(gas in a) b)
{%e %b %d %f %a %c}

Remove Members

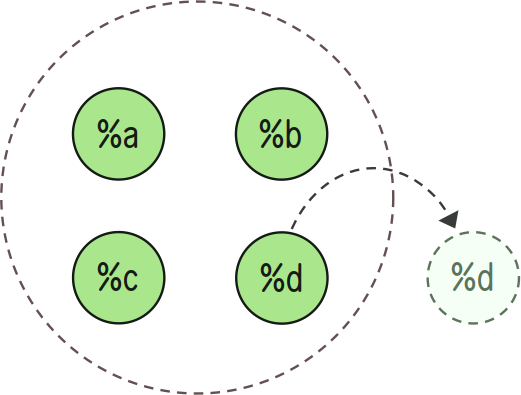
++del:in removes an element x from a set A.

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c %d])
  `(set @tas)`(~(del in a) %d)
{%b %a %c}

Membership

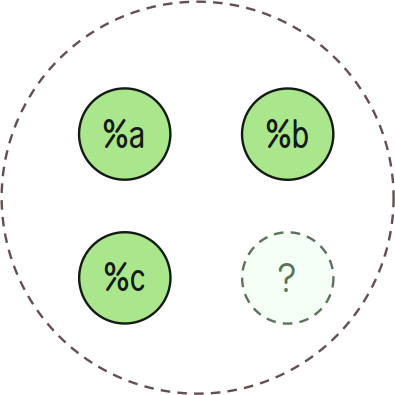
++has:in checks if an element x is in a set A.

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  (~(has in a) %a)
%.y

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  (~(has in a) %d)
%.n

Size

++wyt:in produces the number of elements in A as an atom (width).

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  ~(wyt in a)
3

Export as List

++tap:in produces the elements of set A as a $list. The order is the same as a depth-first search of the $set's representation as a $tree, reversed.

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  ~(tap in a)
~[%c %a %b]

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
    =/  b  `(list @tas)`~[%d %e %f]
    ~(tap in `(set @tas)`(~(gas in a) b))
~[%c %a %f %d %b %e]

Set Relations

First we consider the elementary operations between two sets.

Union (A ∪ B)

$$A \cup B \equiv \{ x : x \in A \text{ or } x \in B \}$$

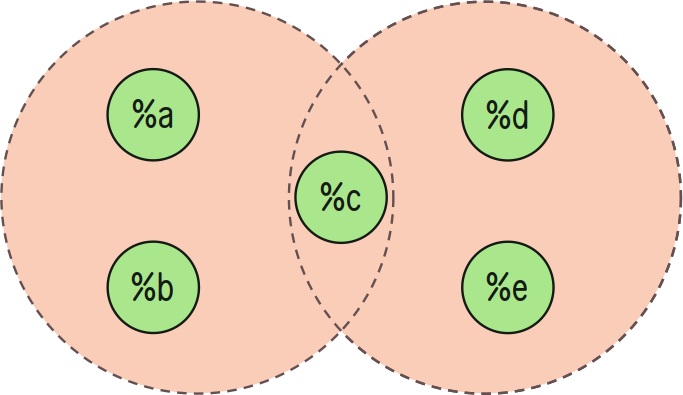
++uni:in produces a set containing all values from A or B. The types of A and B must match.

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  =/  b  `(set @tas)`(silt `(list @tas)`~[%c %d %e])
  `(set @tas)`(~(uni in a) b)
{%e %b %d %a %c}

Intersection (A ∩ B)

$$A \cap B \equiv \{ x : x \in A \text{ and } x \in B \}$$

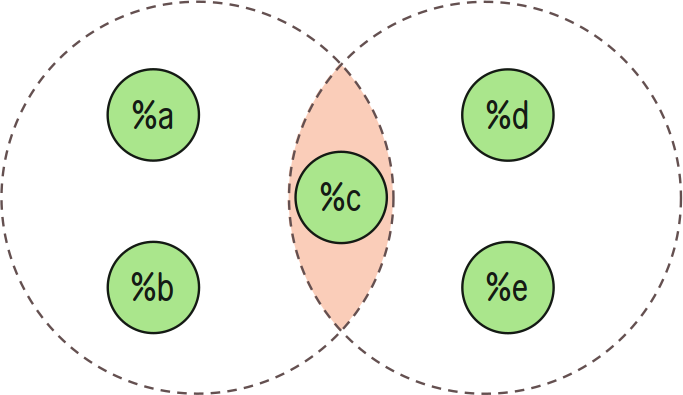
++int:in produces a set containing all values from A and B. The types of A and B must match.

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  =/  b  `(set @tas)`(silt `(list @tas)`~[%c %d %e])
  `(set @tas)`(~(int in a) b)
{%c}

If two sets are disjoint, then their intersection is ∅.

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  =/  b  `(set @tas)`(silt `(list @tas)`~[%d %e %f])
  `(set @tas)`(~(int in a) b)
{}

Complement (Aꟲ)

$$A^{\textrm{C}} = X \backslash A \equiv {x \in X; x \notin A}$$

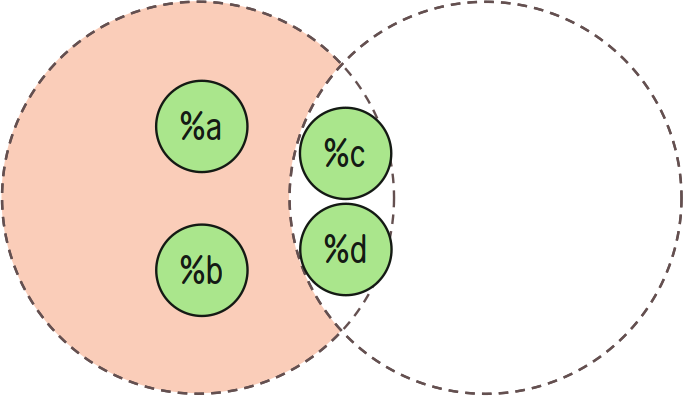
The complement of a set A, Aꟲ, may be found using ++dif (difference).

For instance, if X = {a, b, c, d} and A = {c, d}, then Aꟲ = {a, b}.

> =/  x  `(set @tas)`(silt `(list @tas)`~[%a %b %c %d])
  =/  a  `(set @tas)`(silt `(list @tas)`~[%c %d])
  `(set @tas)`(~(dif in x) a)
{%b %a}

Symmetric Difference (A Δ B)

$$A \bigtriangleup B \equiv \{x : x \text{ belongs to exactly one of } A \text{ and } B\}$$

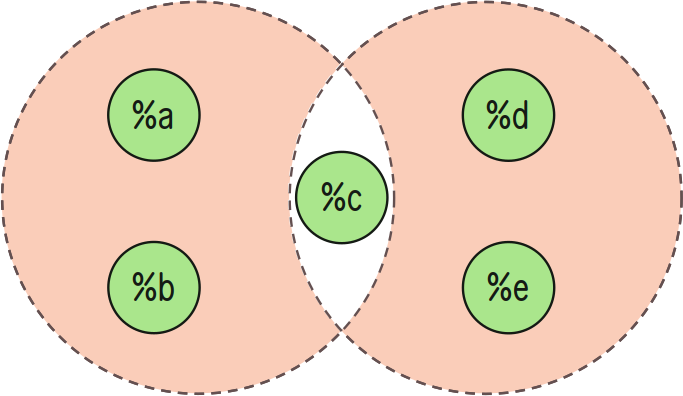
The symmetric difference of two sets A and B consists of those elements in exactly one of the sets. Use ++uni:in with ++dif:in to identify this set.

For instance, if A = {a, b, c} and B = {c, d, e}, then A Δ B = {a, b, d, e}.

=/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
=/  b  `(set @tas)`(silt `(list @tas)`~[%c %d %e])
=/  lhs  (~(dif in a) b)
=/  rhs  (~(dif in b) a)
`(set @tas)`(~(uni in lhs) rhs)

Set Operations

Logical AND (∧)

++all:in computes the logical AND on every element in set A against a logical function f, producing a flag.

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  (~(all in a) (curr gth 32))
%.y

Logical OR (∨)

++any:in computes the logical OR on every element in set A against a logical function f, producing a flag.

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  (~(any in a) (curr gth 32))
%.y

Operate with Function

++run:in applies a function f to every member of set A.

> =/  a  `(set @tas)`(silt `(list @tas)`~[%a %b %c])
  (~(run in a) @ud)
{98 97 99}

Accumulate with Function

++rep:in applies a binary function f to every member of set A and accumulates the result.

=/  a  `(set @ud)`(silt `(list @ud)`~[1 2 3 4 5])
    (~(rep in a) mul)
b=120

While there are a few other set functions in +in, they are largely concerned with internal operations such as consistency checking.